The ELECTROLEVEL is an electronic gravity sensing transducer which can be used in various configurations to measure the motions of a ship at sea. This application note examines the accuracy of such measurement and discusses the background to measuring ships motions.
A ship at sea is subject to six oscillating motions:
-
Pitch: angular motion about the ships transverse axis.
-
Roll: angular motion about the ships longitudinal axis.
- Yaw: angular motion in the horizontal plane containing the
projection of the longitudinal axis, about
the mean course.
- Surge: fore and aft movement of the C.G. of the ship after
subtracting mean speed.
- Sway: transverse movement of the C.G. of the ship measured in
the horizontal plane.
- Heave: vertical movement of the C.G. of the ship.
These motions are produced by wave action and evidently depend on the heading and size of the ship with respect to the waves.
Because the ELECTROLEVEL is pendulous device it senses accelerations as well as gravity.
These accelerations cause errors in angular reading.
The magnitude of these errors is examined in the following analysis in which a
simple model of ships motion is used to identify the chief causes of error in practical situations.
|
Mathematical Analysis
Consider an ELECTROLEVEL sensor mounted on board ship at a height h and lateral displacement b from the axis of a rolling motion represented by
q = q 1 sin w t (see figure 1).
The polar coordinates of the sensor are R q, and the corresponding cartesian coordinates are
X=R sinq Y=R cos
q
q = q 0+ q 1 sin
w t
An ELECTROLEVEL subject to accelerations x" ,y" produces an output which is interpreted as an effective angle q eff
where q eff=q true - arctan(x"/(g+y"))
|
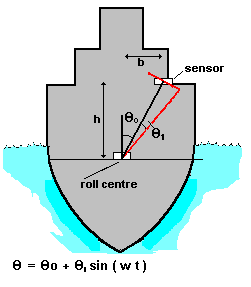 Figure 1
Figure 1
|
(see application note ELECTROLEVEL AS AN ACCELEROMETER).
After some reduction neglecting terms q13 and smaller,
error angle = + q1
(1+hw 2/g) sin
(w t) + bw 2/g. q12 cos (2
w t)-(hb/g2)w 4 q12 sin2 (w t) .......(1)
From this equation we can draw the following practical conclusions:-
To measure static angles, e.g. trim, heel or alignment angles, a time constant filter circuit will reduce the first two error terms to an arbitrarily small value, at the expense of a slower response time
(see application note TIME CONSTANT IN ELECTROLEVEL CIRCUITS).
However the third term has a non-zero d.c. error value of 1/2(hb/g2)w 4 q12 which will not be attenuated by any filter method.
If b and h can be chosen near zero i.e. by mounting the ELECTROLEVEL sensor near the pitch and roll centre of the vessel, all acceleration errors can be reduced. If this mounting position is not possible, then equation 1 gives an estimate of the error, (which is negligible for many applications.)
E.g. for a 6° roll amplitude with 10 second period the d.c. error term is 1.6 arc seconds per metre2 of displacement.
So if h = b = 10 metres the resulting datum error caused by these acceleration effects is approximately 3 minutes of arc.
To measure dynamic angles - e.g. pitch and roll amplitudes such as q1 equation 1 shows the values of h, b must be reduced to low level by mounting the sensor at the pitch and roll centre of the vessel.
If this is not possible then the error terms in equation 1 can be reduced by taking readings from an array of suitably placed sensors and computing the true angle of roll.
|
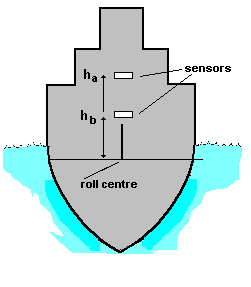
Fig 2 shows such an arrangement where the roll centre of the ship is inaccessible. Two sensors are mounted at heights ha hb above the roll centre (where b = 0) The measured angles are thus:
q a = q1 (1+ha w 2/g) sin (w t)
qb = q1 (1+hb w 2/g) sin (w t)
And the combination
(hb qa - ha qb.)/( hb - ha )= q1 sin (w t)
is the true roll angle.
Note that error cancellation is frequency independent and hence applies for any oscillatory roll motion experienced by the ship. Practical limits to error cancellation techniques like this are determined by
- (a) flexure of the ship
- (b) the matching of the two sensor characteristics over their operating range.(This can be made quite close by selecting the sensors.)
- (c) third order effects caused by coupling of surge, yaw, heave and sway motions.
The complexity of the latter are such that a particular application should be evaluated by computer simulation if high accuracy measurements are to be made.
|
Figure 2
|
Dynamic response of the ELECTROLEVEL
To a first approximation the ELECTROLEVEL behaves like a simple pendulum with a natural frequency of oscillation fn and damping factor d. The natural frequency of the standard ELECTROLEVEL sensors is between 1 and 2.5 Hz and is ideally suited to following low frequency wave-induced motion. The damping factor d is between 0.6 and 0.9 at room temperature. Exceptionally, for a very small vessel a correction might have to be made for higher frequency oscillations
.
Summary and Miscellaneous Comments
The most effective method of measuring true roll and pitch angles on board ship is to :-
(a) Mount the transducer at the centre of minimum pitch movement.
(b) If this is not possible then to mount the sensor in the same horizontal plane as the pitch/roll centre so that h=0.
(c) Failing a, b, use two transducers at different heights and an error compensation circuit to remove acceleration terms.
Note that it is possible to measure the linear acceleration terms, heave surge and sway with accelerometers and to electronically double integrate these terms to give a reading of displacement.
Note also that in some applications concerned with stability of on-deck loads, etc., it can be desirable to mount the ELECTROLEVEL sensors at the load location, since there they will give an apparent pitch/roll reading directly related to the inertial forces causing load instability.
Tilt Measurements' Engineers are available for discussion of any possible
applications and have many years experience in the design of systems for
customers from a diverse range of industries.
|
All information herein is believed to be correct but no
liability is accepted by Tilt Measurement Limited for any
application in respect of fitness of purpose, infringement of
intellectual property rights,or consequential loss or damage
howsoever caused.
|

|

|

|
 Download Data Sheet as .PDF File (33Kbytes)
Download Data Sheet as .PDF File (33Kbytes)
|
ã
2008 Tilt Measurement Limited
|